はじめに
近年、AI(人工知能)について話題になることが増えましたね。人によっては、AIに関し、自社開発、外部企業への開発委託または共同研究開発等を検討したり実施したりする機会も増えてきていることでしょう。
でも、法務担当者等、エンジニア以外の方の中には、「AIって実際のところ、何をしているの?何を計算しているんだろう?」と、具体的なイメージを持てない方もいるのではないでしょうか?
また、そもそも「技術とか理系の話題にはアレルギーが…。」という方もいるかもしれません。
しかし、AI技術について理解があいまいなまま業務を遂行している場合、次のようなリスクが考えられます。
- AI開発プロジェクトやAIを利用したビジネスにおけるリスクの洗い出し、評価、対応策等リスクマネジメントが不十分になるおそれ
- エンジニアとの間のコミュニケーションが不正確、不十分になるおそれ
- 「AI・データの利用に関する契約ガイドライン」等のツールを十分に使いこなせないおそれ
そこで、元・東大理系の弁護士が、法務担当者等の非エンジニアの方向けに、AI技術の基礎を、ディープラーニング(深層学習)を題材とし、具体的にわかりやすく解説します。
なお、いくつか数式は出てきますが、その意味内容がわかるように具体的に説明し、高校数学レベルの知識でわかるようにしています。
そして、この記事をきっかけに、技術や科学に対するアレルギーをなくし、さらにAIの学習を進めて理解を深化させ、AI開発プロジェクトやAIを利用したビジネスのリスクマネジメントの向上、エンジニアとのコミュニケーションの円滑、ガイドライン等のツールの有効活用等につなげていただければ幸いです。
なお、AI開発プロジェクトやAIを利用したビジネスに関する契約書の作成・リーガルチェックのポイントについては、「AI契約ガイドラインと2021年モデル契約書に学ぶAI開発契約のポイント!弁護士が法務担当者に向けて解説」をご覧ください。
AI(人工知能)、機械学習とは?
AI(人工知能。Artificial Inteligence)について、専門家や研究者の間でも、確立した学術的な定義や合意がありません。研究者により様々です(総務省・ICTスキル総合習得教材3-5「人工知能と機械学習」、平成28年度情報通信白書参照)。
そして、機械学習とは、データから規則性や判断基準を学習し、それに基づき未知のものを予測、判断する技術とAIに関わる分析技術を指す言葉です。なお、機械学習の定義もあいまいな面があります。
この機械学習の技術の1つに、近年話題のディープラーニング(深層学習)があります。ディープラーニングは、後述するニューラルネットワークという分析手法の一種であり、高精度の分析や活用を可能にした手法です。
なお、機械学習は大きく、教師あり学習(代表的な分析手法として回帰分析、決定木等)、教師なし学習(代表的な分析手法としてk平均法、アソシエーション分析等)、強化学習の3つに分類されますが、ディープラーニングは、教師あり学習、教師なし学習、強化学習のすべてに適用できることが特徴です。
では次に、ニューラルネットワークとディープラーニングについて見ていくこととしましょう。
ニューラルネットワークとディープラーニング(深層学習)
(注)技術的な内容については、「C++で学ぶディープラーニング」(藤田毅)を参考にしました。
ニューラルネットワークとは?
ニューラルネットワークは、脳のニューロン(神経細胞)のネットワークをモデル化したものです。
ニューロン(神経細胞)の概要
ニューロン(神経細胞)には、樹状突起と呼ばれる部分と軸索と呼ばれる部分があります。樹状突起は他のニューロンから情報を受け取る部分(入力)、軸索は他のニューロンに情報を伝える部分(出力)です。
ニューロンは、他のニューロンからの電気刺激を受け取り、これがある値(閾値)を超えると興奮し、他のニューロンに電気刺激を伝えます。
このようなニューロンのネットワークをモデル化したものが、次に紹介するニューラルネットワークです。
なお、ニューロンのイメージ図等につきましては、例えば中外製薬様のホームページ等で見ることができます。
ニューラルネットワーク(ディープラーニング(深層学習))の具体例
下図に、ニューラルネットワークの例を示します。
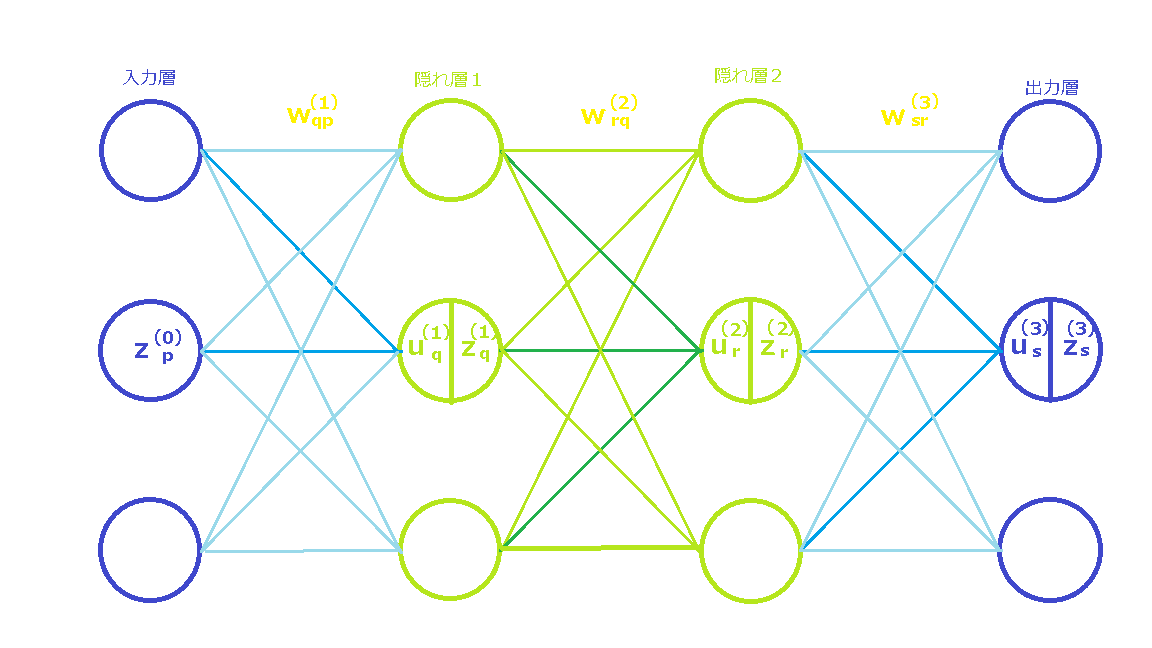
3つ丸印(「ユニット」と呼びます。)が1つ層を構成し、横に並んでいます。
慣例的に、一番左の層を「入力層」と呼び、一番右の層を「出力層」と呼びます。これらの中間の層を「隠れ層」と呼びます。
なお、この図では、簡単のため、3つのユニットが各層を構成し、また隠れ層を2層としていますが、各層を構成するユニット数はいくつでも構いません。また、各層を構成するユニット数がそれぞれ異なっても構いません。さらに、隠れ層は1層でも2層でも、それ以上でも構いません。
特に、隠れ層が2つ以上のニューラルネットワークは、ディープラーニングと呼ばれています。
もう少し詳しく見ていきましょう。
入力層
入力層の上から1番目のユニット、2番目のユニット及び3番目のユニットの出力を、それぞれ
\[z^{(0)}_1, z^{(0)}_2, z^{(0)}_3\]
としましょう。
図中では、\(p\)番目のユニットの出力が\(z^{(0)}_p\)である旨記載しています。右上と右下の\({(0)}\)と\(p\)という添え字は、左から0番目の層の\(p\)番目のユニットであることを示しています。
なお、この例では入力層のユニット数は3つですが、例えば、100×100ピクセルの白黒画像データ(画像の各点(10,000個!)の色の濃さのデータから構成されます。)を入力しようとするならば、入力層に10,000個のユニットが必要になります。
隠れ層1
次に、入力層の各ユニットの出力が、隠れ層1の各ユニットに伝わっています。
ここで、入力層の\(p\)番目のユニットから隠れ層1の\(q\)番目のユニットへの伝わりやすさを\(w^{(1)}_{qp}\)とします。これを「重み」と呼びます。
そうすると、隠れ層1の\(q\)番目のユニットが入力層の各ユニットから受け取る出力の合計を、次のように表すことができます。
\[\sum^3_{p=1}w^{(1)}_{qp}z^{(0)}_p\]
ここで、\(\sum\)は、\(p=1\)から\(3\)までの各項を合計することを表しています。
例えば、隠れ層1の1番目のユニットの場合だと、
\[\sum^3_{p=1}w^{(1)}_{1p}z^{(0)}_p=w^{(1)}_{11}z^{(0)}_1+w^{(1)}_{12}z^{(0)}_2+w^{(1)}_{13}z^{(0)}_3\]
となります。
さて、ユニットには、ニューロンのように振舞ってもらいたいところです。
ニューロンは、閾値を超える入力があると興奮するのでしたね。
そこで、隠れ層1の\(q\)番目のユニットの閾値を\(b^{(1)}_q\)としましょう。
以上をまとめ、隠れ層1の\(q\)番目のユニットへの入力\(u^{(1)}_q\)を次のように表すこととしましょう。
\[u^{(1)}_q=\sum^3_{p=1}w^{(1)}_{qp}z^{(0)}_p+b^{(1)}_q\]
例えば、隠れ層1の1番目のユニットの場合だと、次のようになります。
\[u^{(1)}_1=\sum^3_{p=1}w^{(1)}_{1p}z^{(0)}_p+b^{(1)}_1=w^{(1)}_{11}z^{(0)}_1+w^{(1)}_{12}z^{(0)}_2+w^{(1)}_{13}z^{(0)}_3+b^{(1)}_1\]
なお、\(b^{(1)}_q\)の前の符号がマイナスではなくてプラスとなっていますが、間違えではありません。\(b^{(1)}_q\)は正の値でも負の値でもいいので、ニューロンでの閾値を一般化しているといえます。また、ここがマイナスだと、後々計算する際にプラスとマイナスが入り混じって見づらくなることもあります。
次に、ユニットの振る舞いを表す関数を考えましょう。このような関数を活性化関数と呼びます。
例えば、入力が0未満ならばユニットの出力が0、0より大きければ出力が1となるような関数が考えられます。
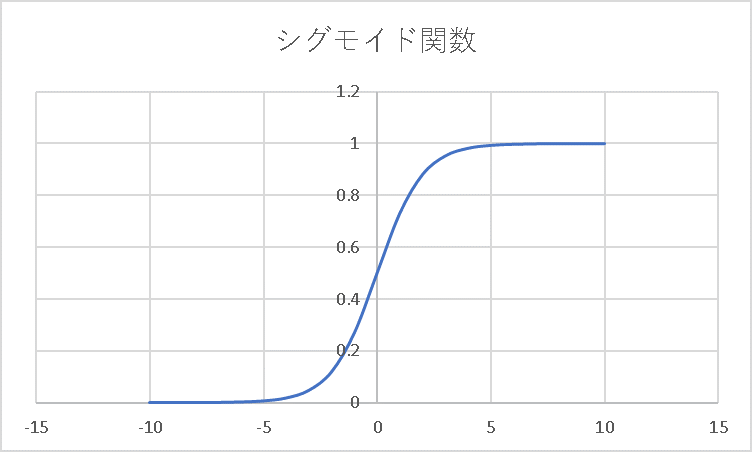
そのようなものに近い例として、シグモイド関数と呼ばれる関数があります。
\[f(x)=\frac{1}{1+e^{-x}}\]
この関数は、\(x=0\)の前後で、急激に0から1に変化する関数です。
シグモイド関数以外にも、様々な関数が活性化関数に用いられています。
ここでは、隠れ層1の活性化関数を、\(f^{(1)}(x)\)と表すこととします。
以上をまとめると、隠れ層1の\(q\)番目のユニットの出力\(z^{(1)}_q\)を、次のように表すことができます。
\[z^{(1)}_q=f^{(1)}(u^{(1)}_q)\]
隠れ層2
同様の考察を行うと、隠れ層2の\(r\)番目のユニットへの入力と出力について、次の結果が得られます。
\[u^{(2)}_r=\sum^3_{q=1}w^{(2)}_{rq}z^{(1)}_q+b^{(2)}_r\]
\[z^{(2)}_r= f^{(2)}(u^{(2)}_r)\]
出力層
また同様に、出力層の\(s\)番目のユニットへの入力について、次の結果が得られます。
\[u^{(3)}_s=\sum^3_{r=1}w^{(3)}_{sr}z^{(2)}_r+b^{(3)}_s\]
ここで、\(u^{(3)}_s\)は、一般に、整数等のとびとびの値ではなく、連続的な値になります。
そして、例えば、気温から売上を予測したいとか、いくつかの財務指標から営業利益率を予測したいといった回帰問題では、ニューラルネットワークの出力が、とびとびの値ではなく連続的な値で大丈夫です。
ですので、\(u^{(3)}_s\)をそのまま\(s\)番目のユニットの出力としておいて良さそうです。
\[z^{(3)}_s=f^{(3)}(u^{(3)}_s)=u^{(3)}_s\]
これに対して、画像を猫、犬、その他に分類する等の分類問題の場合では様子が変わってきます。
例えば、出力層の1番目、2番目、3番目のユニットの出力が、それぞれ猫である確率、犬である確率、その他である確率と解釈できると良さそうです。
そして、確率なので0から1の値を取ってほしいです。
また、猫である確率、犬である確率、その他である確率を合計すると1になってほしいです。
そこで、\(s\)番目のユニットの出力\(z^{(3)}_s\)を、次のようにすることが考えられます。
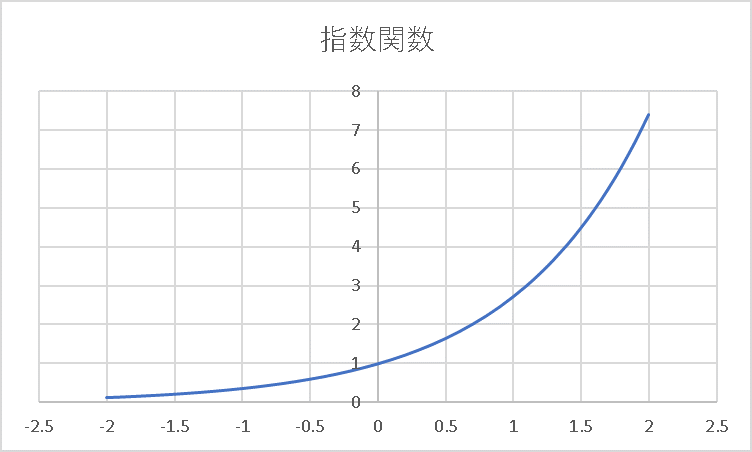
\[z^{(3)}_s=f^{(3)}(u^{(3)}_s)=\frac{e^{u^{(3)}_s}}{e^{u^{(3)}_1}+e^{u^{(3)}_2}+e^{u^{(3)}_3}}\]
ここで、\(e\)は自然対数の底(\(2.718…\))です。
指数関数は正の値を取ります。そのため、\(z^{(3)}_s\)の分子は正の値、分母は、(分子+正の数)であることから、分子より大きな正の値になります。その結果、\(z^{(3)} _s\)は0から1の間の値となります。
また、
\[z^{(3)}_1+z^{(3)}_2+z^{(3)}_3=1\]
となります。
なお、この記事では指数関数を使った計算を特に行いませんので、「ふーん。」と思って見ておいていただければ大丈夫です。
小括
以上では、ニューラルネットワークにおいて、入力層から入力された数値データが、左の層から右の層へと、どのように数値計算されて伝わり、最終的に出力層から数値データが出力されるかを、簡単な例を用いて見てきました。
そして、入力された数値データに対してどのような数値データが出力されるかは、\(w^{(1)}_{qp},w^{(2)}_{rq},w^{(3)}_{sr},b^{(1)}_q,b^{(2)}_r,b^{(3)}_s\)といったパラメータによって決まります。
そうであるならば、これらのパラメータをうまく調整することにより、入力した画像データに対して猫である確率を得たり、財務指標から営業利益率の予想データを得たりできそうです。
このパラメータの調整プロセスを「学習」といいます。
次に、どうやってパラメータを調整していくのか、説明します。
パラメータを調整しよう(学習)
誤差関数(損失関数)
方針としては、ニューラルネットワークによる出力データの「正解からの遠さ」を数字で評価し、この「正解からの遠さ」が最小となるようにパラメータを調整すると良さそうです。この「正解からの遠さ」を表す関数(\(E\))を、「誤差関数」、「損失関数」等といいます。
さて、入力されたサンプルデータ\(z^{(0)}_p(p=1,2,3)\)に対し、出力層から得られるデータは\(z^{(3)}_s(s=1,2,3)\)でした。
他方、サンプルデータに対し、正解のデータ(教師データ)が、\(t_s(s=1,2,3)\)であったとしましょう。
ここで、例えば先ほど言及した営業利益予測モデルならば(出力層のユニットは1つだとして)、
\(t_1=\)正解である営業利益率
となります。
画像を猫、犬、その他に分類するモデルならば、
\[t_1=1,t_2=0,t_3=0\] 等になります。
営業利益率予測等、出力データが連続的な値で大丈夫な場合、誤差関数として、しばしば二乗誤差が用いられます。
\[E=\frac{1}{2}\{(t_1-z^{(3)}_1)^2+(t_2-z^{(3)}_2)^2+(t_3-z^{(3)}_3)^2\}=\frac{1}{2}\sum^3_{s=1} (t_s-z^{(3)}_s)^2\]
なお、\(\frac{1}{2}\)があるのは、\(E\)を微分すると出てくる数字の2を約分し、計算しやすくするための工夫です。
正解から遠ければ遠いほど\(E\)の値は大きくなり、正解に近ければ近いほど\(E\)は0に近づきますね。
他方、分類問題の場合、次のような関数が用いられます(ソフトマックス・クロスエントロピー誤差関数と呼ばれます。)。
\[E=-(t_1\log z^{(3)}_1+t_2\log z^{(3)}_2+t_3\log z^{(3)}_3)=-\sum^3_{s=1}t_s\log z^{(3)}_s\]
分類問題では、\(t_s\)は0または1です。例えば、先ほど言及した、猫、犬、その他に分類するモデルの場合であって、正解が猫であったとき、教師データは\(t_1=1,t_2=0,t_3=0\)となります。そうすると、
\[E=-t_1\log z^{(3)}_1\]
となります。
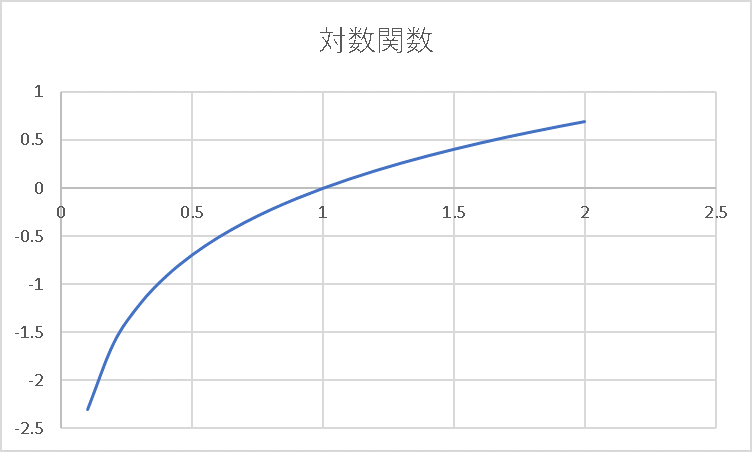
対数関数は、\(xy\)平面の\((1,0)\)を通る右上がりのグラフでした。そして、\(x=1\)未満では\(y\)はマイナスの値になります。加えて、\(x\)が0に近づけば近づくほど、\(y\)の値はマイナス方向にどんどん大きくなります。
そのため、\(z^{(3)}_1\)が正解である1から遠いほど(つまり0に近いほど)、\(E\)の値は大きくなります。
なお、対数関数が出てきましたが、この記事では対数関数を使った計算を特に行いませんので、「ふーん。」と思って見ておいていただければ大丈夫です。
誤差関数(損失関数)を最小化するパラメータを探そう
ニューラルネットワークが出した回答の「正解からの遠さ」を表す誤差関数\(E\)が決まりました。\(E\)は、\(w^{(1)}_{qp},w^{(2)}_{rq},w^{(3)}_{sr},b^{(1)}_q,b^{(2)}_r,b^{(3)}_s\)といったパラメータの関数といえます。
次は、\(E\)が最小となるパラメータを見つければ良さそうです。
では、そのようなパラメータをどうやって探せばいいでしょうか?
方針はシンプルです。
まずは例え話でアイデアをお伝えします。
日本で一番標高が高い地点を探すとしたら、どうやって探しますか?
富士山が一番高いということは知らないという前提でお願いします。
まず、今、地面に立っているとしましょう。そこは坂道のこともあるかもしれません。坂道でないとしても、地面も完全に平らというものでもなく、いくらかは傾いていることでしょう。
そこで、傾いている方向に数メートル移動しましょう。地面にビー玉を置いて転がる方向と逆の方向に移動するイメージです。そうすれば、移動前に比べて、標高が少し高い地点に移動することができます。
これを何度も何度も繰り返せば、おそらくいつかは富士山の山頂にたどり着くことができそうですね。
もちろん、例えば、京都からスタートしたら、嵐山を登ることとなり、富士山にたどり着けないこともあるかもしれません。
しかし、スタート地点を工夫したりすることで、うまく富士山の山頂にたどり着けそうです。
では、地面の傾きはどうやったらわかるでしょうか?
ここで、微分が必要になります。
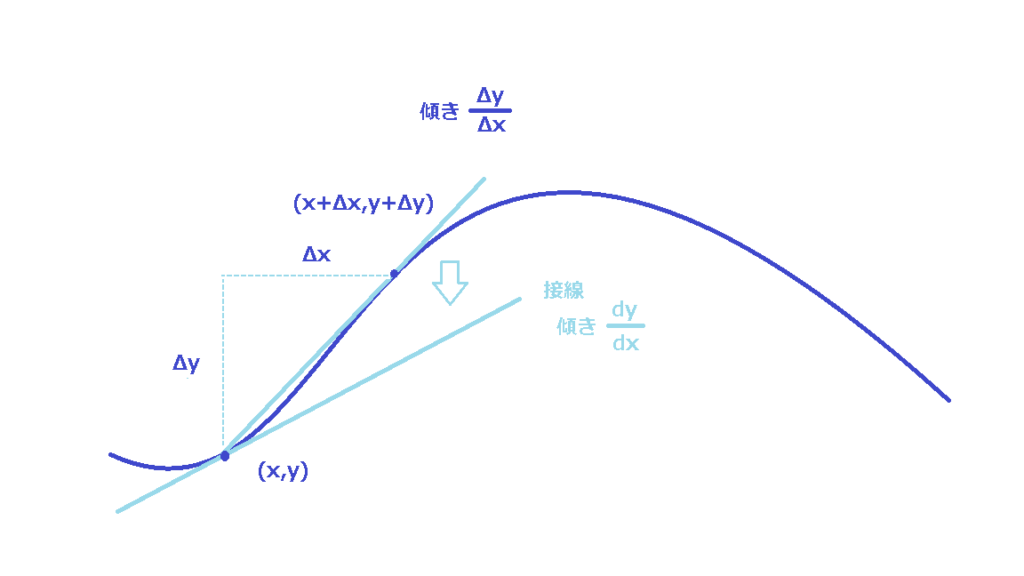
まず、1変数関数の微分について復習しましょう。
グラフ上のある点\((x,y)\)から\(\Delta x\)だけ移動したとき、\(y\)がもとの値からどれだけ変化したか?を表すのが\(\Delta y\)でした。
そして、点\((x,y)\)と点\((x+\Delta x,y+\Delta y)\)を結んだ直線の傾きは\(\displaystyle\frac{\Delta y}{\Delta x}\)でした。
次に、\(\Delta x\)をどんどん小さくしていくと、\(\Delta y\)も小さくなっていきます。
そして、\(\displaystyle\frac{\Delta y}{\Delta x}\)がどんどん近づいていく先の値が微分\(\displaystyle\frac{dy}{dx}\)でした。いわば、点\((x,y)\)付近でのグラフの変化率でした。\(\Delta x\)が十分小さければ、\(\Delta y\)を\(\displaystyle\frac{dy}{dx}\Delta x\)で近似できましたね。
またこのとき、点\((x,y)\)と点\((x+\Delta x,y+\Delta y)\)を結んだ直線は、点\((x,y)\)での接線にどんどん近づいていきます。
ですので、幾何学的にいえば、微分は点\((x,y)\)での接線の傾きといえます。
次に、日本で一番標高の高い場所を探すケースに戻って考えてみましょう。
ある地点\((x,y)\)は、京都タワーから東に\(x\)メートル、北に\(y\)メートルの地点を表しているとしましょう(上記の1変数関数のお話では、\(y\)は\(x\)の関数でしたが、話題が変わって\(x\)と\(y\)は独立したパラメータになっているので、ご注意ください。)。
そうすると、ある地点\((x,y)\)での標高は\(x\)と\(y\)の関数\(H(x,y)\)といえます。
では、この場合の傾きをどう考えたらいいでしょうか?次のようにシンプルに考えることができます。
ある地点\((x,y)\)から真東に\(\Delta x\)だけ移動した場合の標高の変化を\(\Delta H\)としましょう。
そして、\(\Delta x\)をどんどん小さくしていったときに\(\displaystyle\frac{\Delta H}{\Delta x}\)が近づく値を考えればいいです。その近づいて行った先の値、真東にちょっぴり移動したときの標高の変化率を\(\displaystyle\frac{\partial H}{\partial x}\)と書きます(このように、他の変数を動かさずにある変数をちょっぴり動かしてする微分を偏微分といいます)。
同様に真北に\(\Delta y\)だけ移動した場合を考えて、真北にちょっぴり移動したときの標高の変化率を\(\displaystyle\frac{\partial H}{\partial y}\)と書きます。
図形的には、これらの\(\displaystyle\frac{\partial H}{\partial x},\frac{\partial H}{\partial y}\)は、地点\((x,y)\)での接平面の傾きを表します。
これで地面の傾きがわかりました。
\(\displaystyle\frac{\partial H}{\partial x}\)がプラスなら東に少し進みましょう(ビー玉は西側に転がっていくことでしょう。)。マイナスなら西に少し進みましょう(ビー玉は東側に転がっていくことでしょう。)
同時に、\(\displaystyle\frac{\partial H}{\partial y}\)がプラスなら北に少し進み、マイナスなら南に少し進みましょう。
具体的には、\(\eta\)を1メートル等、適当に決めた距離とし、
地点\((x,y)\)から地点\(\displaystyle (x+\eta\frac{\partial H}{\partial x},y+\eta\frac{\partial H}{\partial y})\)に移動すれば良さそうです。
これで移動の度に、それまでよりも標高の高い地点に移動できそうですね。
ここで本題である誤差関数を最小化するパラメータの探し方に戻りましょう。
日本で一番標高が高い地点を探すアルゴリズムと同様のアルゴリズムで探すことができます。
まず、入力層、隠れ層1及び隠れ層2に、常に出力が1となる0番目のユニットをそれぞれ付け加えましょう(\(z^{(0)}_0=z^{(1)}_0=z^{(2)}_0=1\))。また\(b^{(1)}_q,b^{(2)}_r,b^{(3)}_s\)を、それぞれ\(w^{(1)}_{q0},w^{(2)}_{r0},w^{(3)}_{s0}\)と書き表すことにしましょう。これは、次のように重み\(w\)と\(b\)を同じように取り扱えて便利になるので行っています。
\[u^{(1)}_q=\sum^3_{p=0}w^{(1)}_{qp}z^{(0)}_p\]
\[u^{(2)}_r=\sum^3_{q=0}w^{(2)}_{rq}z^{(1)}_q\]
\[u^{(3)}_s=\sum^3_{r=0}w^{(3)}_{sr}z^{(2)}_r\]
そして、\(l\)番目の層の\(i\)番目のユニットと\((l-1)\)番目の層の\(j\)番目のユニットとの間の重み\(w^{(l)}_{ij}\)について、サンプルデータを入力する都度、次のものに置き換えれば良さそうです(確率的最急降下法と呼ばれる解法です。なお、いわば「一番標高の低い地点」を探す問題であることから、\(\eta\)の前はマイナスになっています。)。
\[w^{(l)}_{ij}-\eta\frac{\partial E}{\partial w^{(l)}_{ij}}\]
では、この偏微分(勾配)をどうやって計算すればいいでしょうか?
これは、次に説明する誤差逆伝播法により計算することができます。
誤差逆伝播法でパラメータの計算をしよう
ここからは直感的に説明します。
数式の計算が続きます。お急ぎの方は、次の「オートエンコーダ(自己符号化器)による事前学習」に進んでくださっても大丈夫です。
さて、\(\displaystyle\frac{\partial E}{\partial w^{(l)}_{ij}}\)は、\(w^{(l)}_{ij}\)を\(\Delta w^{(l)}_{ij}\)だけちょっぴり変化させたときの\(E\)の変化率でした。
そうすると、\(E\)の変化\(\Delta E\)を、次のように近似できます。
\[\Delta E\sim\frac{\partial E}{\partial w^{(l)}_{ij}}\Delta w^{(l)}_{ij}\]
ここで、「\(\sim\)」は、「ほぼ等しい」ことを意味する記号です。
他方、\((l-1)\)番目の層の\(j\)番目のユニットと\(l\)番目の層の\(i\)番目のユニットの間の重み\(w^{(l)}_{ij}\)が\(\Delta w^{(l)}_{ij}\)だけ変化したときの、\(l\)番目の層の\(i\)番目のユニットへの入力\(u^{(l)}_i\)の変化\(\Delta u^{(l)}_i\)を、次のように近似できます。
\[\Delta u^{(l)}_i\sim\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}\Delta w^{(l)}_{ij}\]
そして、\(l\)番目の層の\(i\)番目のユニットへの入力\(u^{(l)}_i\)が\(\Delta u^{(l)}_i\)だけ変化したときの、誤差関数\(E\)の変化\(\Delta E\)を、次のように近似できます。
\[\Delta E\sim\frac{\partial E}{\partial u^{(l)}_i}\Delta u^{(l)}_i\]
これに先ほどの\(\Delta u^{(l)}_i\)の式を代入すると、
\[\Delta E\sim\frac{\partial E}{\partial u^{(l)}_i}\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}\Delta w^{(l)}_{ij}\]
これと最初の\(\Delta E\)の式を見比べると、次のことがわかります。
\[\frac{\partial E}{\partial w^{(l)}_{ij}}=\frac{\partial E}{\partial u^{(l)}_i}\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}\]
詳細は省略しますが、\(\displaystyle\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}\)を計算すると、次のようになります。
\[\frac{\partial u^{(l)}_i}{\partial w^{(l)}_{ij}}=z^{(l-1)}_j\]
それでは次に、\(\displaystyle\frac{\partial E}{\partial u^{(l)}_i}\)を計算していきましょう。
先ほど述べたとおり、\(l\)番目の層の\(i\)番目のユニットへの入力\(u^{(l)}_i\)が\(\Delta u^{(l)}_i\)だけ変化したときの、誤差関数\(E\)の変化\(\Delta E\)を、次のように近似できます。
\[\Delta E\sim\frac{\partial E}{\partial u^{(l)}_i}\Delta u^{(l)}_i\]
他方、\(l\)番目の層の\(i\)番目のユニットへの入力\(u^{(l)}_i\)が\(\Delta u^{(l)}_i\)だけ変化したとき、出力\(z^{(l)}_i\)の変化\(\Delta z^{(l)}_i\)を、偏微分を使って次のように近似できます。
\[\Delta z^{(l)}_i\sim\frac{\partial z^{(l)}_i}{\partial u^{(l)}_i}\Delta u^{(l)}_i\]
そして、\(l\)番目の層の\(i\)番目のユニットの出力\(z^{(l)}_i\)が\(\Delta z^{(l)}_i\)だけ変化したとき、\((l+1)\)番目の層の各ユニットへの入力\(u^{(l+1)}_k\)の変化\(\Delta u^{(l+1)}_k\)を、次のように近似できます。
\[\Delta u^{(l+1)}_k\sim\frac{\partial u^{(l+1)}_k}{\partial z^{(l)}_i}\Delta z^{(l)}_i\]
さらに、\((l+1)\)番目の層の各ユニットへの入力\(u^{(l+1)}_k\)が\(\Delta u^{(l+1)}_k\)だけ変化したとき、誤差関数\(E\)の変化\(\Delta E\)を、次のように近似できます。
\[\Delta E\sim\sum_k\frac{\partial E}{\partial u^{(l+1)}_k}\Delta u^{(l+1)}_k\]
これらをまとめると、\(l\)番目の層の\(i\)番目のユニットへの入力\(u^{(l)}_i\)が\(\Delta u^{(l)}_i\)だけ変化したときの、誤差関数\(E\)の変化\(\Delta E\)を、次のようにも近似できます。
\[\Delta E\sim\sum_k\frac{\partial E}{\partial u^{(l+1)}_k}\frac{\partial u^{(l+1)}_k}{\partial z^{(l)}_i}\frac{\partial z^{(l)}_i}{\partial u^{(l)}_i}\Delta u^{(l)}_i\]
これと、先ほど示した\(\Delta u^{(l)}_i\)に対する誤差関数\(E\)の変化\(\Delta E\)の式とを見比べると、次のことがわかります。
\[ \frac{\partial E}{\partial u^{(l)}_i}=\sum_k\frac{\partial E}{\partial u^{(l+1)}_k}\frac{\partial u^{(l+1)}_k}{\partial z^{(l)}_i}\frac{\partial z^{(l)}_i}{\partial u^{(l)}_i}\]
ここで、\(\displaystyle\frac{\partial u^{(l+1)}_k}{\partial z^{(l)}_i}\)を計算すると、次のようになります。
\[\frac{\partial u^{(l+1)}_k}{\partial z^{(l)}_i}=w^{(l+1)}_{ki}\]
そして、式を見やすくするために、次のように\(\delta^{(l)}_i\)を定義します。
\[\delta^{(l)}_i=\frac{\partial E}{\partial u^{(l)}_i}\]
また、\(\displaystyle\frac{\partial z^{(l)}_i}{\partial u^{(l)}_i}\)を次のように書くことにしましょう。ダッシュは微分することを表しています。
\[\frac{\partial z^{(l)}_i}{\partial u^{(l)}_i}=f’^{(l)}(u^{(l)}_i)\]
そうすると、次の漸化式が得られます。
\[\delta^{(l)}_i=\sum_k\delta^{(l+1)}_k w^{(l+1)}_{ki}f’^{(l)}( u^{(l)}_i)\]
ここで、(更新前の)\(w^{(l+1)}_{ki}\)は既知です。
また、\(f^{(l)}(x)\)も既知ですから、\(f’^{(l)}(u^{(l)}_i)\)も計算し得ます。
そうすると、まず\(\delta^{(3)}_s\)を計算し、次に、これを使って\(\delta^{(2)}_r\)を計算することができます。そうすればさらに、これを使って\(\delta^{(1)}_q\)を計算することができますね。
また、この\(\delta^{(l)}_i\)を使うと、\(\displaystyle\frac{\partial E}{\partial w^{(l)}_{ij}}\)を、次のように表すことができます。
\[\frac{\partial E}{\partial w^{(l)}_{ij}}=\delta^{(l)}_i z^{(l-1)}_j\]
ここで\(z^{(l-1)}_j\)も計算済みでした。
これにて、\(\displaystyle\frac{\partial E}{\partial w^{(l)}_{ij}}\)を計算することができますね。
以上により、\(w^{(l)}_{ij}\)を、どのように調整していけばいいかがわかりました。ここで示した一連の計算過程を誤差逆伝播法といいます。
オートエンコーダ(自己符号化器)による事前学習
これまでに説明したように、ニューラルネットワークでは、誤差逆伝播法により重みを計算することができることがわかりました。これにより、万事解決できそうにも思えます。
しかし、重みの初期値によっては、京都の嵐山から出られないように局所最適解に捕まってしまうことがあり得ます。また、\(\displaystyle\frac{\partial E}{\partial w^{(l)}_{ij}}\)がゼロに近づきすぎて学習が進まなくなったり(勾配消失)、逆に大きくなりすぎてコンピュータ処理ができなくなったり(勾配発散)することもあり得ます。また、ニューラルネットワークがいわば丸暗記しすぎて未知のデータに弱くなることもあり得ます(過学習)。
そして、層が深く(多く)なればなるほど、精度向上が見込まれるのに、学習がうまくいかなくなるという問題がありました。ディープラーニングでは学習がうまく行えませんでした。
しかし、このような問題を超え、ディープラーニングがブレイクし、昨今のAIブーム(第三次)が起こりました。
このようなブレイクスルーのきっかけとなった技術の1つが、次に説明するオートエンコーダによる事前学習でした。
オートエンコーダ(自己符号化器)とは?
オートエンコーダ(自己符号化器)とは、入力層、隠れ層1つ、出力層からなるニューラルネットワークであって、教師データを入力データと同じにして学習するものをいいます。
ここで、隠れ層のユニット数を入力層のユニット数よりも小さくする(あるいは隠れ層のユニット数を自由に決めつつも、いくつかのユニットを無効にして、実質的に入力層のユニット数より小さくする等)して学習します。
いわば、入力層の入力データが、隠れ層に至りいったん情報の一部を失いつつも、出力層で元のデータに復元されるプロセスといえます。そして、入力データがうまく復元できるよう、入力データの特徴が残るよう、学習により重みが調整されます。オートエンコーダの重みは入力データの特徴を保持しているといえます。
事前学習
オートエンコーダによる事前学習は、目的としているニューラルネットワークの1つひとつの層に対し、左から順に、オートエンコーダによる学習を行うものです。
まず、隠れ層1が入力データを再現できるように学習を行い、その結果得られた重みを、目的としているニューラルネットワークの相当する重み\(w^{(1)}_{qp}\)の初期値とします。
次に、入力データに対する隠れ層1の出力を使い、隠れ層2がこれを再現できるように学習を行い、その結果得られた重みを、目的としているニューラルネットワークの相当する重み\(w^{(2)}_{rq}\)の初期値とします。
最後に、出力層を加えて、目的とするニューラルネットワークに対し、通常どおりの学習をします。
このような学習を行うことにより、(理由は未解明ですが)精度向上につながることが経験的に知られています。
また、この例のように、ディープラーニングではデータの特徴自体が自動抽出される点で、従来の機械学習と大いに異なります。従来は、うまく特徴の抽出ができるよう人間の関与が必要でした。
まとめ
この記事では、ニューラルネットワークとは何か、どのようにパラメータを調整(学習)するか、昨今のディープラーニングのブレイクのきっかけとなった技術の1つであるオートエンコーダによる事前学習について解説しました。
従来のソフトウェア開発は演繹的ですが、AI開発は帰納的、経験的ですね。
しばしば、AI技術を利用した成果物の精度は学習データに大きく依存するため、着手前にどんなものが出来上がるか予測することは困難だと言われます。
たしかに、それは難しい部分がありそうですね。学習データが異なれば、得られる重みも異なるのが通常であると思われるからです。
また、AIが判断ミスをし第三者に損害が発生した場合、この損害が、学習データとソフトウェアのどちらに起因するのかを判断することは難しいとも言われます。
たしかに、「AIが入力データからどのようなロジックで出力データを出したのか?」は人間にはわかりにくそうです(ディープラーニングの重みを眺めても、現時点では、直ちに人間が、判断のロジックや理由付けのようなものをを読み取ることは難しそうです。)。このことは、ミスの原因をわかりにくくする要素になり得そうです。
以上で終了しますが、この記事が、法務担当者等、非エンジニアの方がAIについて学ぶ際のお役に立てれば幸いです。





